Зміст
- Що таке правило 4% для виходу на пенсію?
- Як працює правило 4%
- Що нам потрібно змоделювати в Excel
- Модель в Excel
- Традиційний підхід (Лист1)
- Гібридний підхід (Лист2)
- Підхід з єдиною формулою (Лист3)
- Резюме та висновок
- Функції, що використовуються в робочій книзі
- Інструкції
Що таке правило 4% для виходу на пенсію?
Якщо ви займатиметеся плануванням виходу на пенсію, ви, напевно, натрапите на правило 4% для виходу на пенсію, одне з найвідоміших (і часто цитованих) рекомендацій щодо витрат на пенсії. Коротко кажучи, правило 4% намагається просто відповісти на це питання: «Скільки я можу безпечно знімати з моїх пенсійних заощаджень щороку, не вичерпуючи гроші?» Відповідь? Приблизно 4%, з урахуванням інфляції.
Це правило виникло в результаті досліджень, проведених фінансовим консультантом на ім’я Білл Бенген у 1994 році. Його метою було визначити безпечний рівень зняття коштів (SAFEMAX), який дозволив би пенсіонерам підтримувати свій рівень життя протягом 30-річного виходу на пенсію, не вичерпуючи гроші, навіть у періоди поганої ринкової активності та високої інфляції.
На основі історичної реконструкції портфелів пенсіонерів з 1926 року Бенген рекомендував рівень зняття 4% на перший рік, з подальшими коригуваннями на витрати на життя в кожному наступному році. Хоча сам Бенген не називав це «правилом 4%» (і пізніше змінив свою рекомендацію на 4.5%, а потім на 4.7%), назва закріпилася і продовжує використовуватися до сьогодні.
Як працює правило 4%
Застосування правила просте: у вашому першому році виходу на пенсію ви знімаєте 4% від загального балансу портфеля. У кожному наступному році ви коригуєте цю початкову суму на інфляцію, а не перераховуєте 4% від вашого поточного балансу. Наприклад, якщо ви виходите на пенсію з портфелем у 1 мільйон доларів, ви знімете 40,000 доларів у перший рік. Якщо інфляція в тому році становить 3%, ви знімете 41,200 доларів у другий рік і так далі. Ідея полягає в тому, щоб забезпечити передбачуваний дохід, скоригований на інфляцію, зберігаючи портфель у різних ринкових умовах протягом усього періоду виходу на пенсію.
Для тих, хто планує вихід на пенсію, правило 4% слугує як стратегією зняття, так і ціллю заощаджень. Якщо ви знаєте бажаний річний дохід на пенсії, ви можете працювати назад, щоб визначити, скільки вам потрібно заощадити: просто помножте ваш цільовий дохід на 25 (оскільки 4% × 25 = 100%). Хоча правило має багато критиків і може потребувати коригування залежно від індивідуальних обставин, воно залишається корисною відправною точкою для планування виходу на пенсію. Це також чудовий приклад проблеми, яку можна змоделювати в Excel, де ви можете легко тестувати різні сценарії та припущення.
Я не фінансовий консультант. Моя мета не в тому, щоб переконати вас, що правило 4% є найкращим способом планування виходу на пенсію. Моя мета — показати, як ви можете змоделювати таку проблему в Excel різними способами.
Що нам потрібно змоделювати в Excel
Перш ніж перейти до деталей, давайте розглянемо, що нам потрібно змоделювати: починаючи з певного початкового балансу (загальні пенсійні заощадження), нам потрібно розрахувати 4% від початкового балансу, потім щорічно коригувати зняття на інфляцію, додати зростання і показати, як це розвивається протягом 30 років. Нам знадобляться вхідні дані для початкового балансу, рівня зняття, темпу зростання, рівня інфляції, віку на момент виходу на пенсію та кількості років на пенсії, щоб ми могли змінювати ці цифри і бачити, як вони впливають на кінцевий результат:
| Вхідні дані | Опис | Приклад значення |
|---|---|---|
| Початковий баланс | Загальні пенсійні заощадження на початку | 1,000,000 доларів |
| Рівень зняття | Початковий відсоток зняття | 4% |
| Річний темп зростання | Очікувана дохідність портфеля | 7% |
| Рівень інфляції | Щорічне збільшення вартості життя | 2.5% |
| Вік на момент виходу на пенсію | Початковий вік | 65 |
| Роки на пенсії | Тривалість періоду зняття | 30 |
У нашій моделі Excel ми будемо використовувати постійні ставки як для зростання, так і для інфляції протягом усього періоду виходу на пенсію. Це спрощення, яке робить модель легшою для побудови та розуміння. Насправді, доходи портфеля значно варіюються з року в рік (тобто прибутки 20% в один рік, інші втрати 15% в іншому) і ви будете коригувати зняття на основі фактичної річної інфляції, а не на основі припущеної ставки. послідовність цих доходів має велике значення: погана ринкова активність на початку виходу на пенсію є набагато більш руйнівною, ніж ті ж самі погані доходи пізніше. Це називається «ризик послідовності доходів», і саме тому Бенген тестував своє правило 4% на основі історичних ринкових даних, включаючи найгірші сценарії, такі як вихід на пенсію в 1968 році безпосередньо перед великим ринковим падінням і періодом високої інфляції. Наша модель з постійними ставками не відобразить цю реальну волатильність, але вона продемонструє механіку того, як працює правило 4%.
Використовуючи наведені вище вхідні дані, нам потрібно створити «графік зняття», який показує, як змінюється портфель протягом 30 років. Коли ми матимемо графік, ми зможемо розрахувати загальні зняття та фінальний баланс, щоб перевірити, чи пережив портфель вихід на пенсію. Ми також хочемо розрахувати «реальну вартість» кінцевого балансу, скориговану на інфляцію. Нарешті, ми хочемо, щоб графік зняття був динамічним, щоб він розширювався або скорочувався за потреби, коли змінюється кількість років на пенсії. Знімок екрана нижче показує основну ідею. Зверніть увагу, що ключові вхідні дані знаходяться в діапазоні C5:C10. Це змінні, які контролюють виходи. Виходи підсумовуються в діапазоні F5:F9. Графік зняття починається з рядка 13 і охоплює 30 років.
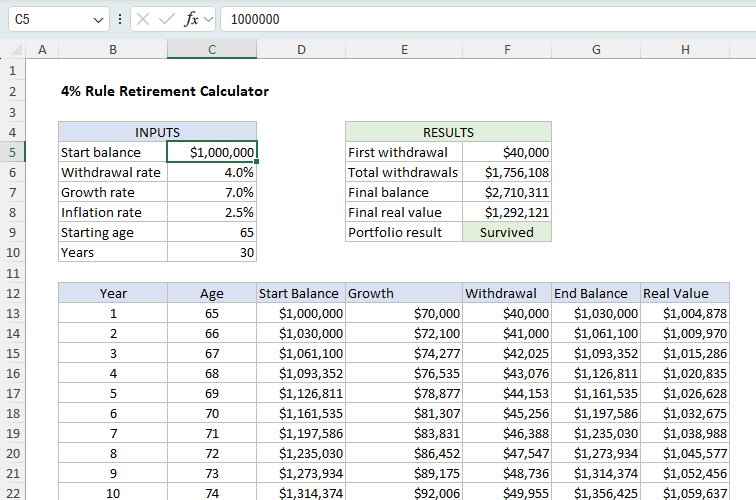
Модель в Excel
Звичайно, існують різні способи змоделювати таку проблему в Excel, особливо оскільки Excel тепер підтримує динамічні масивні формули, які пропонують абсолютно нові способи підходу до багаторядкових розрахунків. Додаткова книга досліджує три різні способи моделювання правила виходу на пенсію у 4%. Усі підходи використовують однакові вхідні дані та дають ідентичні результати, але будують графік зняття коштів все більш просунутими способами — від класичних формул до сучасних динамічних масивів.
- Лист1 — Традиційний підхід — Класичні формули ряд за рядком з відносними та абсолютними посиланнями.
- Лист2 — Гібридний підхід — Одна формула динамічного масиву на стовпець.
- Лист3 — Підхід з однією формулою — Одна формула генерує всю таблицю.
Книга також має четвертий лист з простими інструкціями про те, як користуватися книгою.
Мета цієї вправи не в тому, щоб переконати вас, що один підхід кращий за інший. Мета полягає в тому, щоб розглянути різні способи моделювання такої проблеми в Excel і дослідити деякі переваги та недоліки кожного підходу. Давайте почнемо з традиційного підходу.
У постачанні всі три аркуші мають однакові вхідні дані та дають однакові результати. Єдина різниця полягає в підході, що використовується для побудови графіка зняття коштів та підсумкових результатів у стовпці F. На будь-якому аркуші ви можете змінити вхідні дані в діапазоні C5:C10, щоб побачити, як змінюються результати. Зміни, які ви вносите на одному аркуші не вплинуть на інші аркуші.
Традиційний підхід з формулами (Лист1)
Цей аркуш використовує класичну настройку ряд за рядком — кожен рядок представляє один рік виходу на пенсію, а кожен стовпець містить ключову змінну: Рік, Вік, Початкова сума, Зростання, Зняття, Кінцева сума та Реальна вартість (сума з урахуванням інфляції). Формули копіюються вниз і використовують комбінацію відносних та абсолютних посилань, щоб кожен рядок правильно посилався на результати попереднього року. Для побудови всього графіка зняття коштів на 30 років потрібно більше 200 формул.
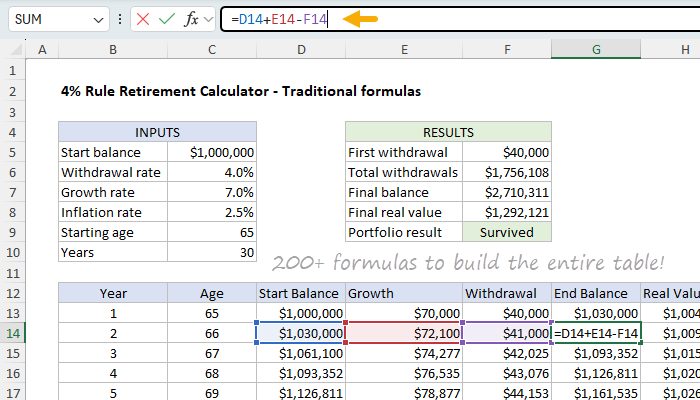
Ось як налаштовані формули:
| Стовпець | Опис | Приклад формули (перший рядок даних) |
|---|---|---|
| B — Рік | Послідовність років | 1 в рядку 13, потім B13+1 |
| C — Вік | Вік у кожному році | =C9 в рядку 13, потім C13+1 |
| D — Початкова сума | Початкова вартість портфеля | =C5 в рядку 13, потім G13 |
| E — Зростання | Зростання портфеля | =D13*$C$7 |
| F — Зняття | Зняття з урахуванням інфляції | =C5*C6 в рядку 13, потім =F13*(1+$C$8) |
| G — Кінцева сума | Кінцева сума року | =D13+E13-F13 |
| H — Реальна вартість | Кінцева сума з урахуванням інфляції | =PV($C$8,B13,0,-G13) |
Підсумкові результати в діапазоні F5:F9 генеруються за допомогою наступних формул:
| Клітинка | Опис | Формула |
|---|---|---|
| F5 | Перше зняття | =C5*C6 |
| F6 | Загальні зняття | =SUM(F13:F100) |
| F7 | Кінцева сума | =LOOKUP(2,1/(G13:G100<>""),G13:G100) |
| F8 | Загальна реальна вартість | =LOOKUP(2,1/(H13:H100<>""),H13:H100) |
| F9 | Результат портфеля | =IF(F7>0,"Survived","Depleted") |
Функція LOOKUP використовується для знаходження останньої непорожньої клітинки в діапазонах G13:G100 та H13:H100. Ці діапазони перевищують необхідний розмір, щоб дозволити таблиці бути розширеною за потреби. Для отримання додаткової інформації про цю формулу дивіться Отримати значення останньої непорожньої клітинки. Функція LOOKUP працює в усіх версіях Excel. Ви можете використовувати той же трюк, щоб витягнути останній рік у стовпці B у C10 (Роки), якщо хочете, але я залишив його як статичне значення, щоб уникнути плутанини. Для отримання додаткової інформації про функцію PV дивіться Функція PV.
Зверніть увагу, що ключовою особливістю цього підходу є те, що формули в рядку 1 графіка часто відрізняються від формул у наступних рядках. Ці формули повинні бути ретельно складені, щоб забезпечити правильне посилання на клітинки, що передбачає використання комбінації відносних та абсолютних посилань. Це також означає, що користувач повинен бути обережним, якщо вносяться зміни до графіка зняття коштів. З іншого боку, цей підхід легко зрозуміти та перевірити, і він працює в усіх версіях Excel.
Переваги та недоліки
| Переваги | Недоліки |
|---|---|
| Легко зрозуміти та перевірити | Потрібно копіювати або розширювати формули вручну |
| Працює в усіх версіях Excel | Фіксований розмір, таблиця не є динамічною |
| Чудово підходить для навчання відносним/абсолютним посиланням | Схильний до помилок посилання, якщо рядки вставляються або видаляються |
Гібридний підхід з формулами (Лист2)
Цей лист використовує формули динамічного масиву для автоматичного генерування кожного повного стовпця даних. Кожен стовпець використовує одну формулу, яка розширюється на необхідну кількість рядків, спочатку прив’язану до Років (C10) вхідних даних. Для побудови всього графіка зняття коштів потрібно 7 формул, по одній на стовпець:
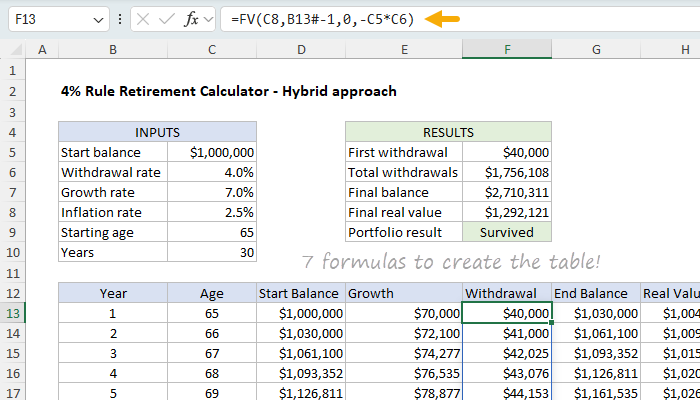
Формули налаштовані так:
| Стовпець | Опис | Формула |
|---|---|---|
| B — Рік | Послідовність років | =SEQUENCE(C10) |
| C — Вік | Початковий вік + послідовність | =SEQUENCE(C10,1,C9) |
| D — Початкова сума | Кінцева сума попереднього року | =VSTACK(C5,DROP(G13#,-1)) |
| E — Зростання | Щорічне зростання | =D13#*C7 |
| F — Зняття | Зняття з урахуванням інфляції | =FV(C8,B13#-1,0,-C5*C6) |
| G — Кінцева сума | Сума після зростання та зняття | =SCAN(C5,F13#,LAMBDA(bal,wd,bal*(1+C7)-wd)) |
| H — Реальна вартість | Сума з урахуванням інфляції | =PV(C8,B13#,0,-G13#) |
Підсумкові результати в діапазоні F5:F9 генеруються за допомогою наступних формул:
| Клітинка | Опис | Формула |
|---|---|---|
| F5 | Перше зняття | =C5*C6 |
| F6 | Загальні зняття | =SUM(F13#) |
| F7 | Кінцева сума | =TAKE(G13#,-1) |
| F8 | Загальна реальна вартість | =TAKE(H13#,-1) |
| F9 | Результат портфеля | =IF(F7>0,"Survived","Depleted") |
Цей підхід у Листі2 є чудовим прикладом того, як формули можуть бути закріплені до існуючого діапазону розширення щоб стовпці автоматично розширювались або звужувались за потреби. Усі формули в стовпцях D до H прив’язані до діапазону spill для років, який починається з клітинки B13, щоб вони автоматично підлаштовувались під правильну кількість рядків за потреби. Діапазон spill для років генерується за допомогою функції SEQUENCE ось так:
=SEQUENCE(C10) // generate years 1 to 30
Якщо кількість років у клітинці C10 змінюється, рядки у стовпці Рік розширяться або звузяться за потреби. Стовпець C (Вік) також створюється за допомогою функції SEQUENCE, яка налаштована на генерацію послідовності віків, що охоплює таку ж кількість років, як і стовпець Рік, починаючи з початкового віку в клітинці C9, і збільшуючи на 1 кожного року.
=SEQUENCE(C10,1,C9) // generate ages 65 to 94
Стовпець D (Початковий баланс) генерується за допомогою розумного поєднання функцій DROP та VSTACK ось так:
=VSTACK(C5,DROP(G13#,-1))
DROP видаляє останній (невикористаний) річний баланс з діапазону spill у стовпці G (Кінцевий баланс). VSTACK потім вставляє початковий баланс у C5 на початку списку та додає річний баланс. Це трохи заплутано, що початковий баланс йде перед кінцевим балансом, і все ж початковий баланс залежить від кінцевого балансу. Але це має сенс, якщо подумати про це — початковий баланс насправді є тим самим, що й кінцевий баланс, зрушений на один рік вниз. Іншими словами, нам потрібен кінцевий баланс, щоб знати початковий баланс у наступному році.
Стовпець E (Зростання) генерується шляхом множення початкового балансу на темп зростання:
=D13#*C7
Стовпець F (Вивід) генерується за допомогою функції FV. Функція FV обчислює майбутню вартість інвестиції на основі початкового основного балансу, фіксованої річної процентної ставки, кількості періодів нарахування та періодичного платежу. У цьому випадку ми використовуємо функцію FV для обчислення майбутньої вартості початкової суми виводу, скоригованої на інфляцію, протягом кількості років у графіку виводу. Формула виглядає ось так:
=FV(C8,B13#-1,0,-C5*C6)
Ставка подається як інфляційна ставка у C8 (2.5%), кількість періодів — це кількість років у графіку виводу мінус 1 B13#-1, теперішня вартість — це початковий баланс, помножений на ставку виводу -C5*C6, а платіж дорівнює 0, оскільки немає періодичних платежів.
Ми використовуємо функцію FV тут, щоб обчислити вивід, скоригований на інфляцію, але ми могли б використовувати еквівалентну формулу в розгорнутому вигляді:
=C5*C6*(1+C8)^(B13#-1). Обидві формули повернуть один і той же результат.
Стовпець G (Кінцевий баланс) генерується за допомогою функції SCAN. Функція SCAN застосовує функцію LAMBDA до серії значень і накопичує результати. У цьому випадку ми використовуємо функцію SCAN для обчислення річних балансів, застосовуючи функцію LAMBDA до початкового балансу та виводу. Формула виглядає ось так:
=SCAN(C5,F13#,LAMBDA(bal,wd,bal*(1+C7)-wd))
Початковий баланс подається як початкове значення в C5, серія значень — це серія виводів у F13#, а функція LAMBDA є LAMBDA(bal,wd,bal*(1+C7)-wd). Функція LAMBDA застосовується до початкового значення та першого значення в серії, і результат повертається. Результат потім використовується як початкове значення для наступної ітерації функції LAMBDA. Цей процес повторюється для кожного значення в серії. З 30 роками в C10 результатом є серія з 30 річних балансів.
Стовпець H (Реальна вартість) генерується за допомогою функції PV. Функція PV обчислює теперішню вартість інвестиції на основі майбутньої вартості, фіксованої річної процентної ставки, кількості періодів нарахування та періодичного платежу. У цьому випадку ми використовуємо функцію PV для обчислення теперішньої вартості річних балансів, скоригованих на інфляцію. Формула виглядає ось так:
=PV(C8,B13#,0,-G13#)
Ставка подається як інфляційна ставка у C8 (2.5%), кількість періодів — це кількість років у графіку виводу B13#, майбутня вартість — це річні баланси у G13#, а платіж дорівнює 0, оскільки немає періодичних платежів.
Ми використовуємо функцію PV тут, щоб обчислити кінцевий баланс, скоригований на інфляцію, але ми могли б використовувати еквівалентну формулу в розгорнутому вигляді:
=G13#/(1+$C$8)^(B13#). Обидві формули повернуть один і той же результат.
Як згадувалось вище, оскільки ці формули пов’язані з діапазонами spill, починаючи з діапазону spill у стовпці B (Рік), усі стовпці будуть змінювати розмір за потреби, якщо кількість років у виході C10 зміниться.
Функції PV та FV в Excel використовують конвенцію грошових потоків, де ви заперечуєте значення, які представляють відтоки. Саме тому теперішня вартість є негативною у функції FV, а майбутня вартість є позитивною у функції PV. Негативний знак забезпечує отримання позитивного результату.
Плюси та мінуси
| Плюси | Мінуси |
|---|---|
| Повністю динамічно — таблиця автоматично змінює розмір | Потребує Excel 365 |
| Одна формула на стовпець, без заблокованих посилань | Залежить від прив’язки до діапазонів spill |
| Чисто, масштабовано та легко читається | Нові функції, такі як SCAN та VSTACK, можуть бути незнайомими |
| Менше формул для управління | Більш абстрактно, ніж підхід рядок за рядком |
Одноформульний підхід (Лист3)
У цьому листі весь графік виводу генерується однією динамічною масивною формулою, яка поєднує LET, SEQUENCE, FV, SCAN, VSTACK та HSTACK. Кожна змінна визначається та повторно використовується в одній виразі, яка розширюється в повну таблицю. Для побудови всього графіка виводу потрібно 9 формул:
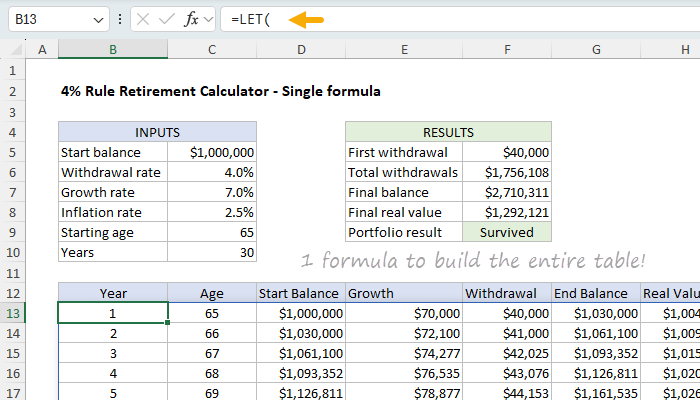
Формула в B13 виглядає ось так:
=LET(
start,C5, wr,C6, gr,C7, ir,C8, age,C9, n,C10,
yrs,SEQUENCE(n),
ages,SEQUENCE(n,1,age),
wds,FV(ir,yrs-1,0,-start*wr),
ends,SCAN(start, wds, LAMBDA(bal,wd, bal*(1+gr)-wd)),
starts,VSTACK(start,DROP(ends,-1)),
growth,starts*gr,
real,PV(ir,yrs,0,-ends),
HSTACK(yrs,ages,starts,growth,wds,ends,real)
)
Ця формула використовує функцію LET для визначення серії змінних, які використовуються для генерації графіка виводу:
| Змінна | Опис |
|---|---|
| start | Початковий баланс портфеля з C5 ($1,000,000) |
| wr | Ставка виводу з C6 (4%) |
| gr | Річна ставка зростання з C7 (7%) |
| ir | Інфляційна ставка з C8 (2.5%) |
| age | Початковий вік з C9 (65) |
| n | Кількість років з C10 (30) |
| років | Послідовність років від 1 до n |
| вік | Послідовність віків, починаючи з віку |
| виведення | Річні виведення, скориговані на інфляцію за допомогою функції FV |
| кінець | Баланси на кінець року, згенеровані за допомогою SCAN |
| початок | Початкові баланси, сформовані з балансу на кінець попереднього року |
| зростання | Річні суми зростання від початкового балансу * ставки зростання |
| реальний | Баланси на кінець року, скориговані на інфляцію за допомогою функції PV |
Підсумкові результати в діапазоні F5:F9 генеруються за допомогою наступних формул:
| Комірка | Опис | Формула |
|---|---|---|
| F5 | Перше виведення | =C5*C6 |
| F6 | Загальні виведення | =SUM(CHOOSECOLS(B13#,5)) |
| F7 | Остаточний баланс | =TAKE(CHOOSECOLS(B13#,6),-1) |
| F8 | Загальна реальна вартість | =TAKE(CHOOSECOLS(B13#,7),-1) |
| F9 | Результат портфеля | =IF(F7>0,"Survived","Depleted") |
Це явно найскладніша формула з трьох підходів, але вона також є найкомпактнішою та найефективнішою. Однією з приємних особливостей побудови формули таким чином є те, що після визначення змінних їх можна використовувати безпосередньо в інших частинах формули замість посилань на комірки, що робить формулу легшою для читання та розуміння. Коротко кажучи, формула працює так:
- Визначте початковий баланс (start), ставку виведення (wr), ставку зростання (gr), ставку інфляції (ir), початковий вік (age) та кількість років (n).
start,C5, wr,C6, gr,C7, ir,C8, age,C9, n,C10 - Згенеруйте послідовність років (yrs) від 1 до n.
yrs,SEQUENCE(n) - Згенеруйте послідовність віків (ages), починаючи з початкового віку.
ages,SEQUENCE(n,1,age) - Згенеруйте серію річних виведень (wds), скоригованих на інфляцію за допомогою функції FV.
wds,FV(ir,yrs-1,0,-start*wr) - Згенеруйте серію балансів на кінець року (ends), застосувавши функцію SCAN до початкового балансу та серії річних виведень.
ends,SCAN(start, wds, LAMBDA(bal,wd, bal*(1+gr)-wd)) - Згенеруйте серію початкових балансів (starts), побудувавши з балансу на кінець попереднього року.
starts,VSTACK(start,DROP(ends,-1)) - Згенеруйте серію річних сум зростання (growth), множачи початковий баланс на ставку зростання.
growth,starts*gr - Згенеруйте серію баланси на кінець року, скориговані на інфляцію (real), застосувавши функцію PV до балансів на кінець року.
real,PV(ir,yrs,0,-ends) - Об’єднайте всі серії в одну таблицю за допомогою функції HSTACK.
HSTACK(yrs,ages,starts,growth,wds,ends,real)
Для деталей про функції, використані у формулі, дивіться розділ Функції, використані в робочій книзі нижче.
Плюси та мінуси
| Плюси | Мінуси |
|---|---|
| Одна формула будує всю таблицю | Потрібні просунуті навички Excel |
| Повністю динамічно, без фіксованих діапазонів | Потрібен Excel 365 |
| Компактно та ефективно | Крутіша крива навчання |
| Єдине джерело правди | Складніше перевіряти комірка за коміркою |
Підсумок та висновок
Усі три аркуші дають один і той же результат: симуляцію року за роком за правилом 4% для виходу на пенсію. Різниця полягає в тому, як будується графік виведення.
- Традиційний (Лист1) будує таблицю крок за кроком, використовуючи відносні та абсолютні посилання.
- Гібридний (Лист2) конструює кожен стовпець за допомогою однієї динамічної масивної формули.
- Одиничний (Лист3) використовує одну динамічну масивну формулу для генерації всієї таблиці.
Кожен підхід є дійсним — ваш вибір залежить від ваших пріоритетів щодо прозорості та гнучкості, а також від вашого рівня комфорту з сучасними функціями Excel. Який підхід вам подобається найбільше?
| Підхід | Сильні сторони | Обмеження | Найкращий випадок використання |
|---|---|---|---|
| Традиційний | Простий, візуальний, легкий для розуміння | Ручна настройка, не динамічний | Викладання, сумісність зі старішими версіями Excel |
| Гібридний | Динамічні масиви, чітка логіка, без заблокованих посилань | Потрібен Excel 365 | Сучасне моделювання в Excel, навчання SCAN та VSTACK |
| Одиничний | Повністю динамічно, одна формула, легко повторно використовувати | Складніше візуально перевіряти | Повторно використовувані шаблони, функції LAMBDA, просунуте моделювання |
Функції, використані в робочій книзі
Моделі в прикріпленій робочій книзі використовують багато функцій Excel, деякі з яких можуть бути вам незнайомі. Нижче наведено список використаних функцій з посиланнями на сторінки з більш детальною інформацією та прикладами. Якщо ви новачок у динамічних масивних формулах, вам також може бути цікава ця стаття: Динамічні масивні формули в Excel.
| Функція | Опис |
|---|---|
| CHOOSECOLS | Витягує конкретні стовпці з масиву |
| DROP | Видаляє рядки або стовпці з початку або кінця масиву |
| FV | Обчислює майбутню вартість інвестиції |
| HSTACK | Об’єднує масиви горизонтально (поряд один з одним) |
| IF | Повертає одне значення, якщо умова істинна, інше — якщо хибна |
| LAMBDA | Створює користувацькі функції за допомогою формульної мови Excel |
| LET | Призначає імена результатам обчислень для використання у формулах |
| PV | Обчислює теперішню вартість інвестиції |
| SCAN | Застосовує функцію до кожного елемента в масиві та повертає проміжні результати |
| SEQUENCE | Генерує послідовність чисел |
| SUM | Додає числа в діапазоні або масиві |
| TAKE | Повертає вказану кількість рядків або стовпців з масиву |
| VSTACK | Об’єднує масиви вертикально (складені один на одного) |
Інструкції
У початковому вигляді всі три аркуші мають однакові вхідні дані та генерують однакові виходи. Єдина різниця полягає в підході до складання графіка зняття коштів. На будь-якому аркуші ви можете змінити вхідні дані в діапазоні C5:C10, щоб побачити, як змінюються виходи. Зміни, які ви вносите на одному аркуші, не вплинуть на інші аркуші. Наприклад, якщо ви зміните початковий баланс у C5 на Аркуші1 з $1,000,000 на $1,500,000, початковий баланс на інших двох аркушах не зміниться.
- Перегляньте 3 аркуші, щоб побачити, як будується графік зняття коштів.
- Змініть вхідні клітинки в колонці C для тестування різних сценаріїв.
- Спостерігайте, як таблиця проекцій оновлюється автоматично.
- Зверніть увагу на Кінцевий баланс у E7 — чи стає він від’ємним?
- Порівняйте Реальну вартість щоб побачити вплив інфляції на купівельну спроможність.
Примітки
Хоча моя модель Excel використовує постійні темпи зростання та інфляції для спрощення, оригінальне дослідження Бенгена було набагато більш суворим. Він використовував фактичні історичні дані з 1926 року, тестуючи понад 50 різних 30-річних періодів виходу на пенсію з реальними річними доходами від акцій, облігацій та інфляційними ставками. Це включало Велику депресію, стагфляцію 1970-х, бикові ринки, ведмежі ринки та все, що між ними. Бенген тестував кілька портфельних розподілів, що варіюються від 0% до 100% акцій, зосереджуючись переважно на 50/50 та 75/25 розподілах акцій до облігацій. Ставка зняття 4% виникла тому, що це була максимальна ставка, яка витримала навіть найгірший історичний сценарій (вихід на пенсію наприкінці 1968 року). Краса його підходу полягала в тестуванні проти фактичних ринкових послідовностей, а не постійних середніх значень.
- Правило 4% передбачає приблизно 60/40 портфель акцій та облігацій.
- Історичний рівень успіху дуже високий протягом 30-річних періодів.
- Ризик послідовності доходів та таймінг ринку не моделюються в цьому робочому зошиті.
- Інші джерела доходу, такі як соціальне забезпечення, не враховуються.
- Податки, витрати на охорону здоров’я та тривалість життя не є частиною цієї моделі.
Додаткове читання
Джерело: https://exceljet.net/articles/modeling-the-4-percent-retirement-rule-in-excel



